√100以上 ピタゴラス の 定理 証明 簡単 472421-ピタゴラスの定理 証明 簡単

ピタゴラスの定理 りゅうのブログ
中学受験の算数では必ず登場しますよね。 そしてヒポクラテスの定理は三平方の定理を知っていれば簡単に証明できます。 ヒポクラテスの定理に比べ圧倒的に三平方の定理のほうが覚えやすい ですし、 今時だと三平方の定理を知っている小学生は多い と 三平方の定理は、別名ピタゴラスの定理と呼ばれ、ピタゴラスが最初に証明したと言われています。 その歴史と証明方法について解説します。 678 中3数学 三平方の定理の証明②(ユークリッドの証明) 三平方の定理の証明ブームを
ピタゴラスの定理 証明 簡単
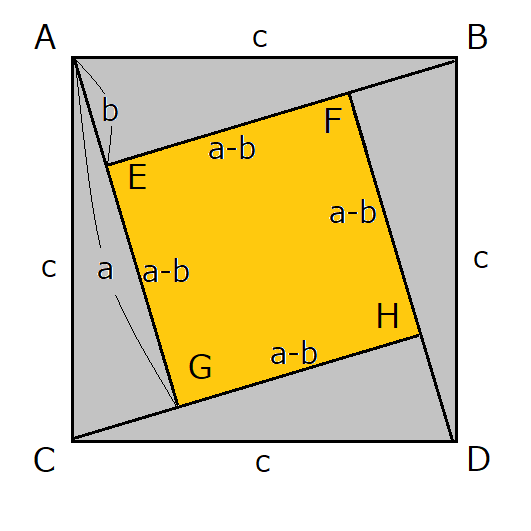
ピタゴラスの定理 証明 簡単- ピタゴラスの定理、ピタゴラス方程式 直角三角形に関して、最も長い一辺( 斜辺 ( しゃへん ) )の長さをz。それ以外の二辺をx、yとすると、三辺の長さの関係は、 x 2 y 2 = z 2 (1) となる。 これは『ピタゴラスの定理』と呼ばれる。ピタゴラスの定理を証明したものである」 とのみ記されている。 この図からどのようにして三平方の定理が 導き出されるのだろうか。 ウモクホ数学に匹敵する学問体系を築き上げた 古代中国の学者に思いをはせながら、 証明方沵を考えてみてください。
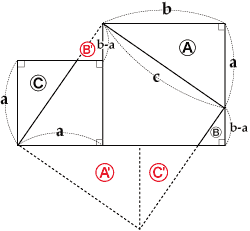
ピタゴラスの定理の拡張のしかた
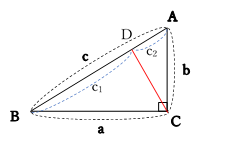
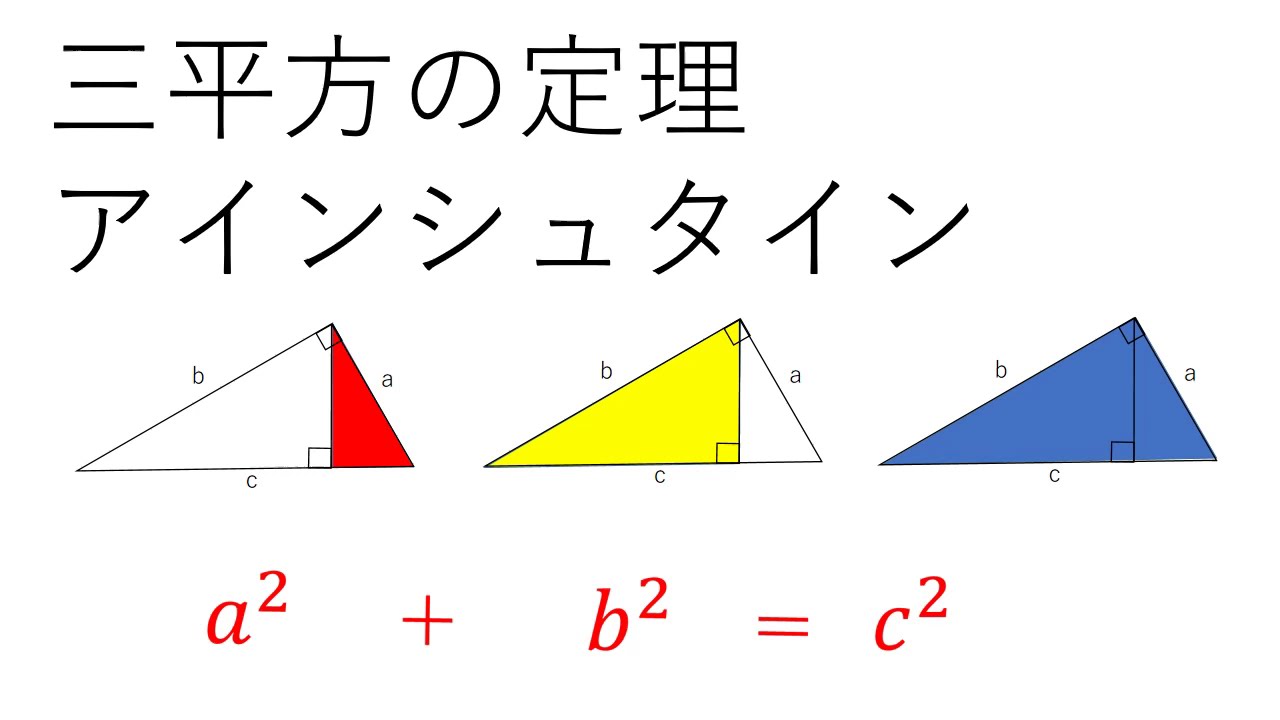
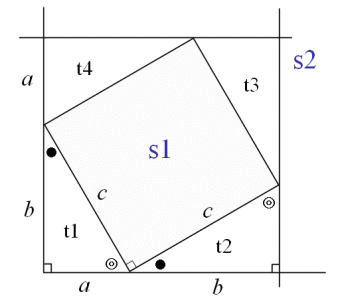
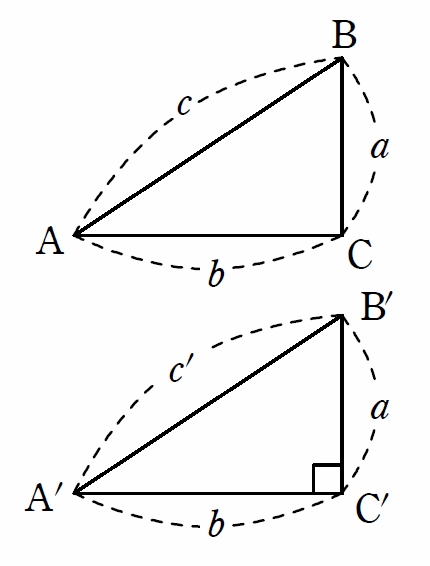
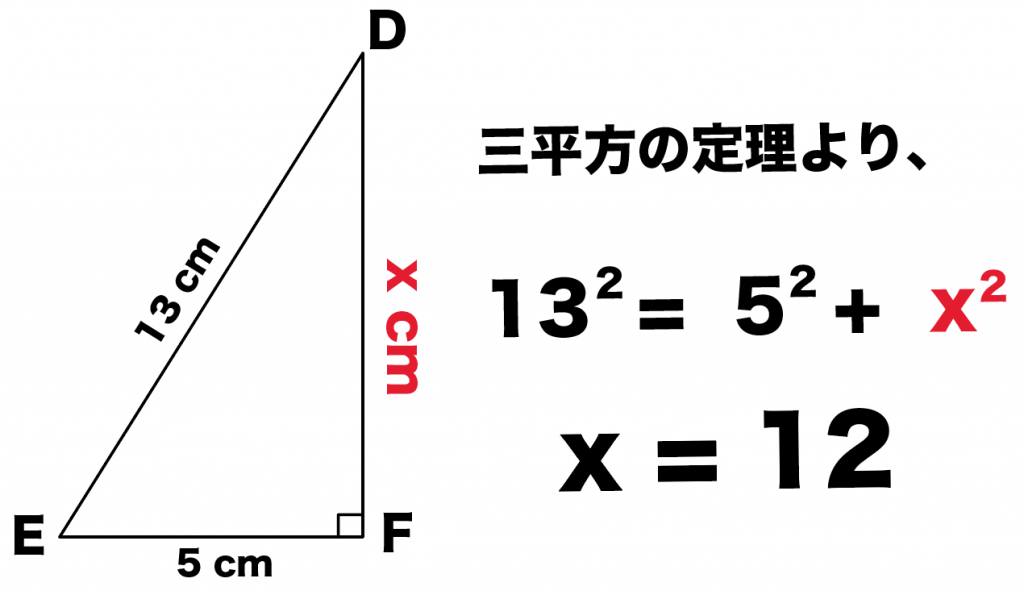
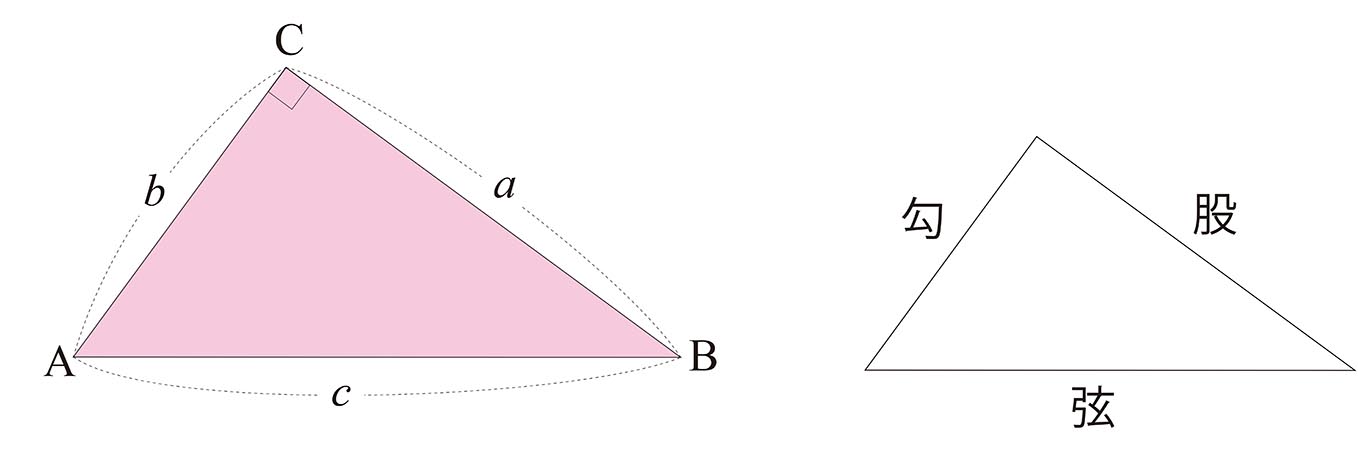
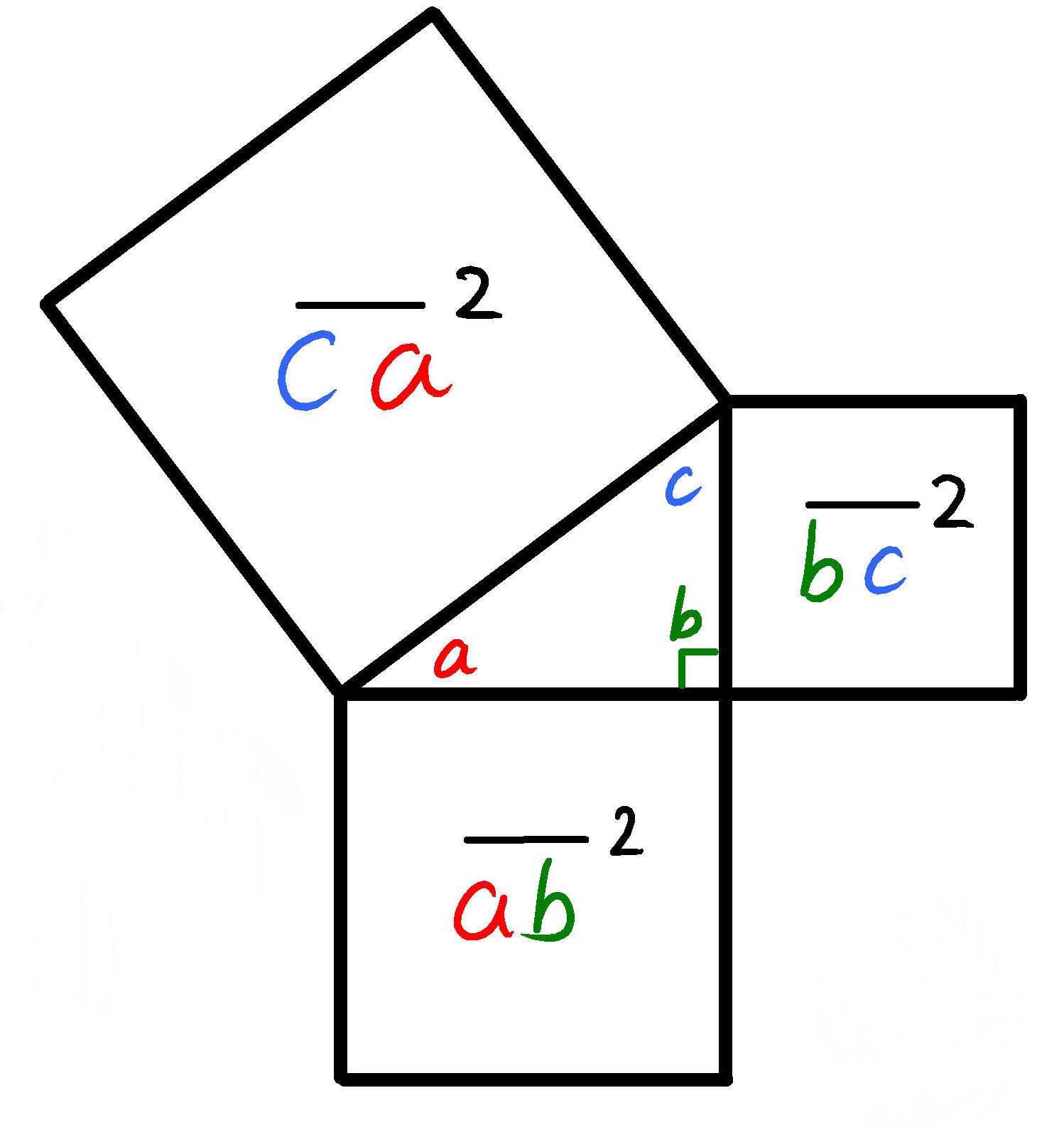
回答 (2件中の1件目) 知りませんが、 「ピタゴラスの定理」そのものが面白いと思っています。 (2次平面)ユークリッド幾何学と(2次元)代数と三角関数に関係する定理だからです。 以下に書きました。 「ピタゴラスの定理」の直感的理解のために 遊風の養生日記Ⅱ三平方の定理とは 三平方の定理とは直角三角形の三辺の長さに関する定理である。 ピタゴラスの定理とも呼ばれる。 三平方の定理 直角三角形の斜辺をc、他の辺をa,bとすると次の関係が成り立つ。 a 2 b 2 =c 2 a b c 三平方の定理の証明 ピタゴラスの定理の証明 0735 日高と申します。 よろしければ、ご指摘いただけないでしょうか。 定理n=2のとき、x^ny^n=z^nは有理数解を持つ。 x^2y^2=z^2を、x^2y^2= (y1)^2 (1)とおく。 (x,yは有理数) (1)を (x1) (x1)=1*2y (2)と変形する。
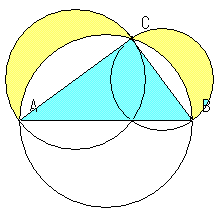
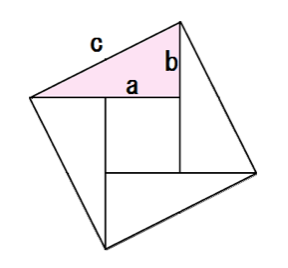
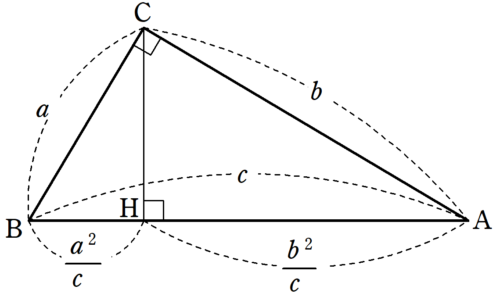
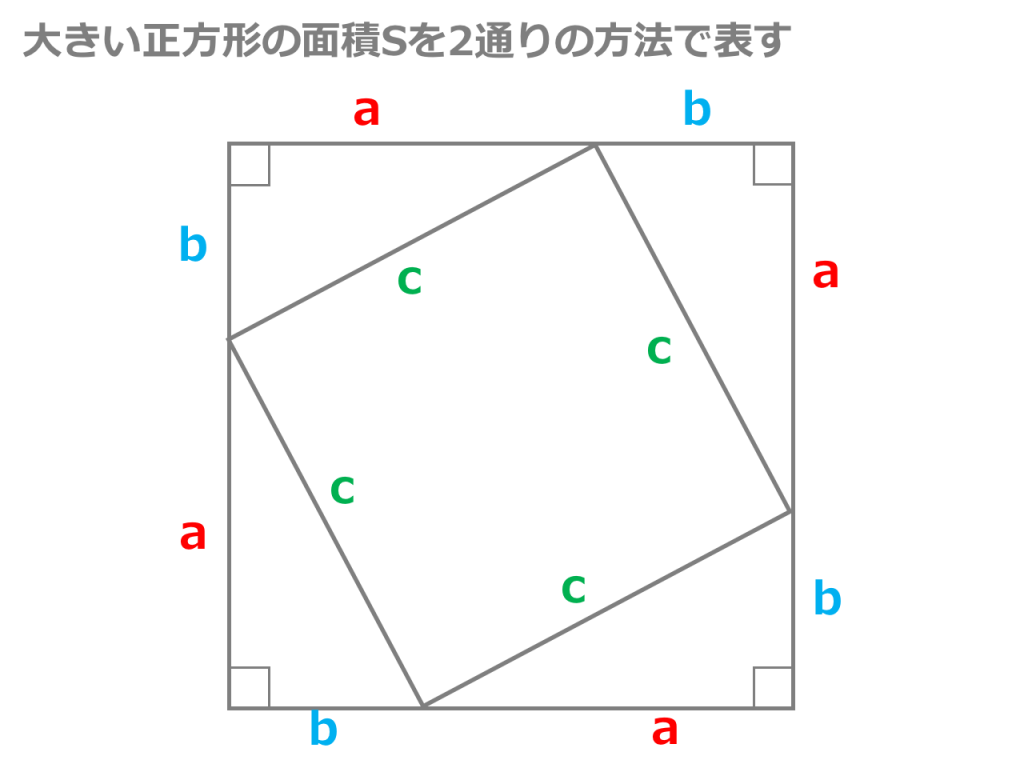
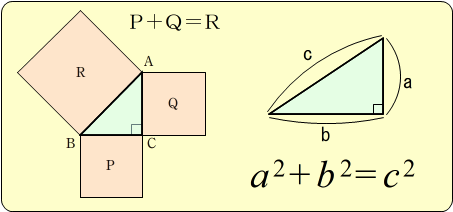
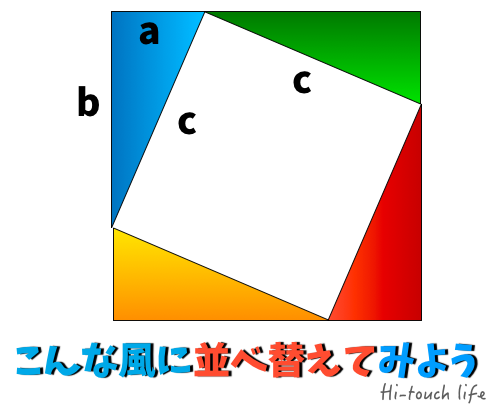
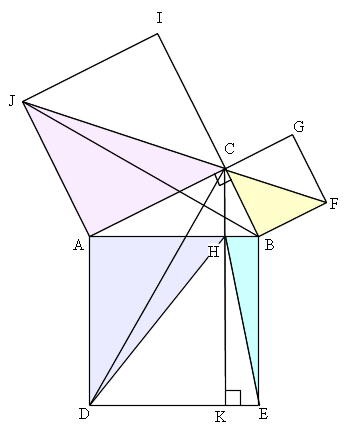
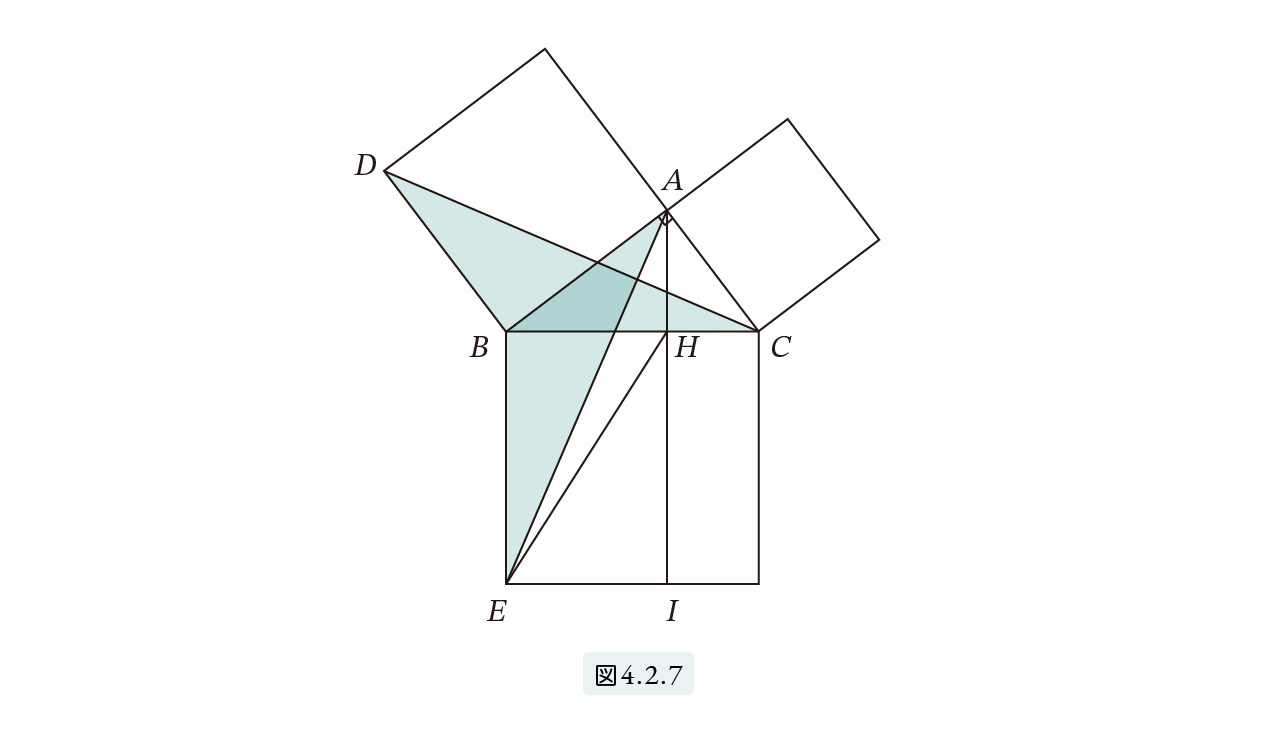
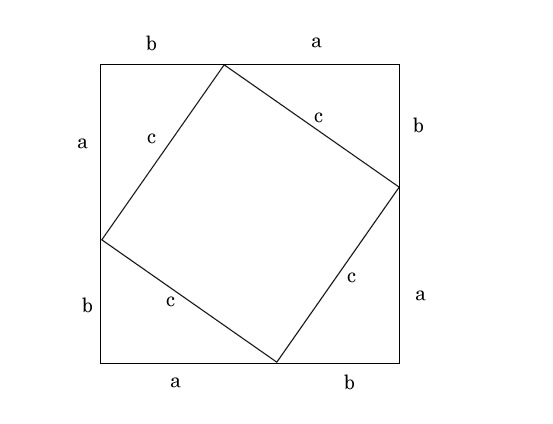
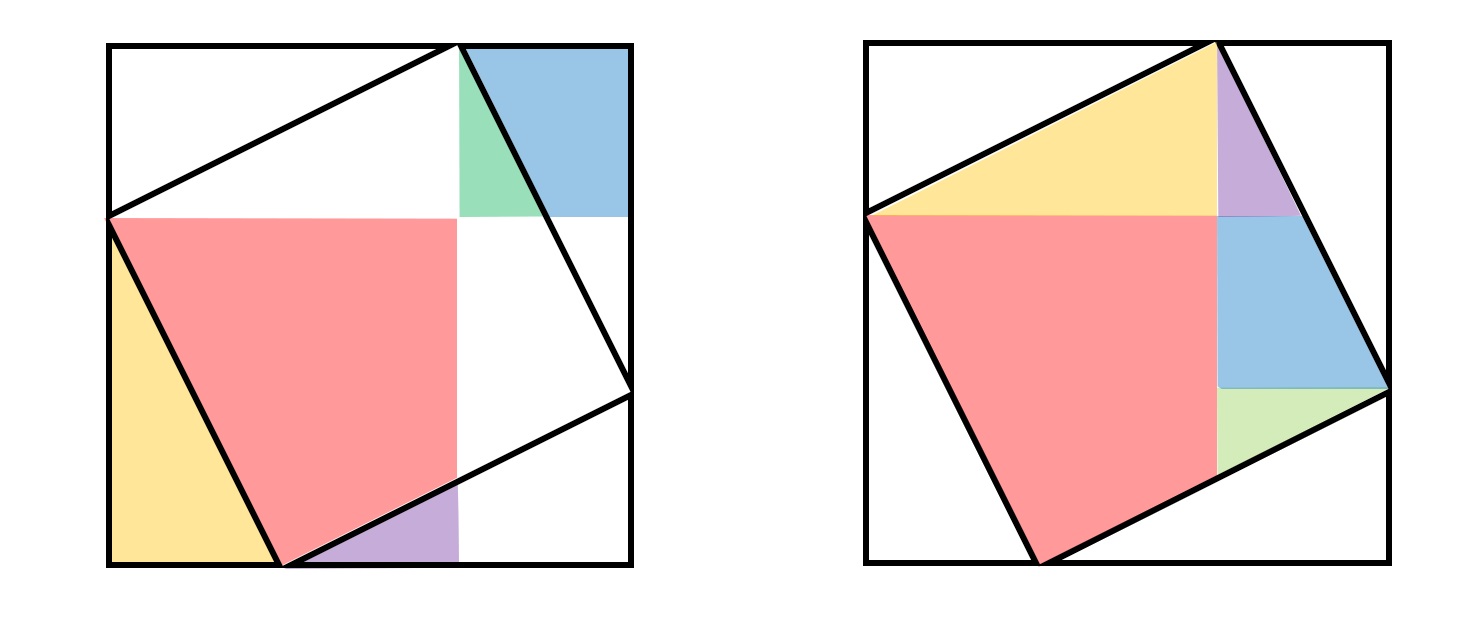
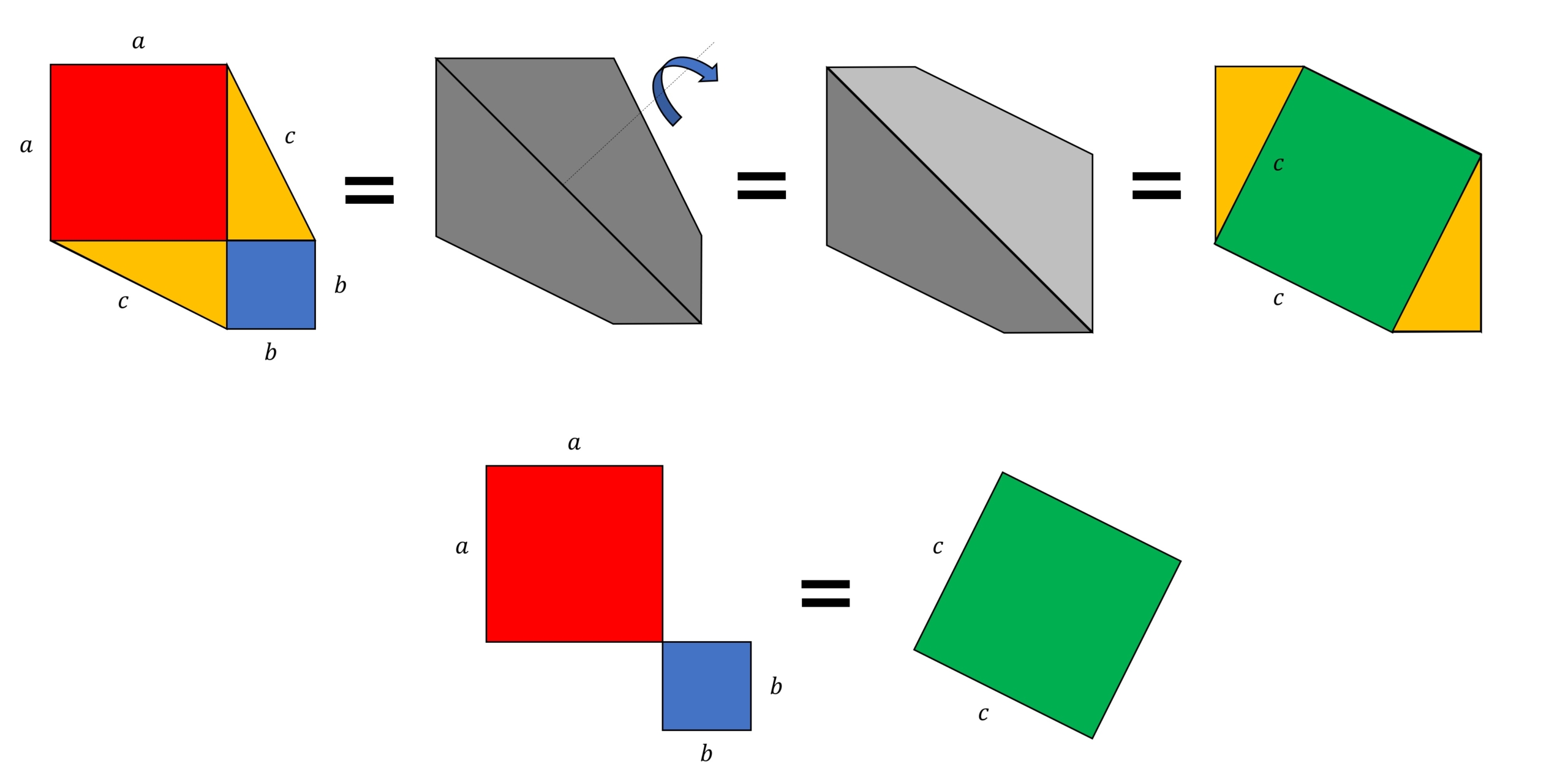
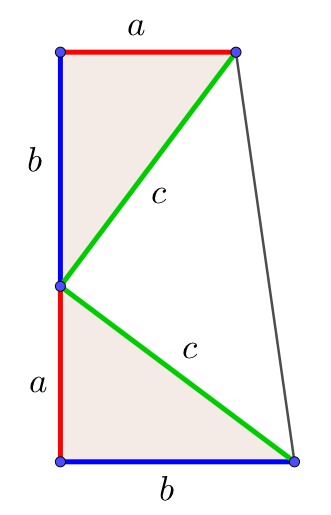
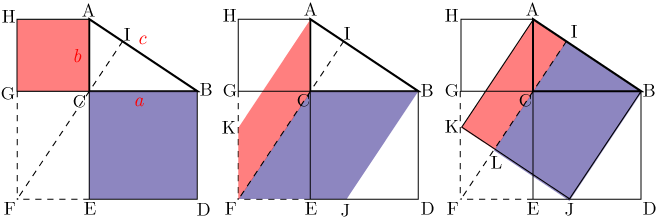
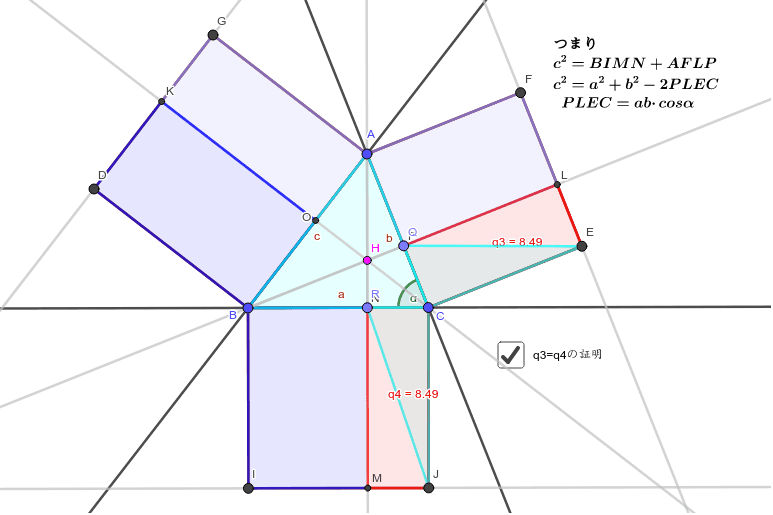
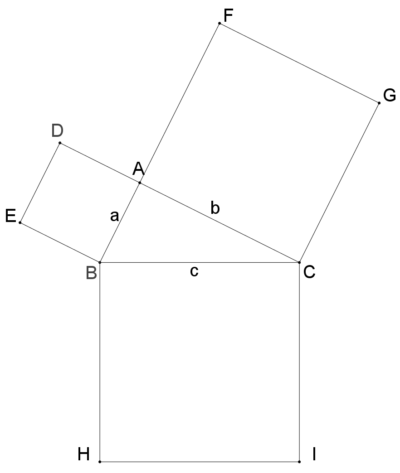
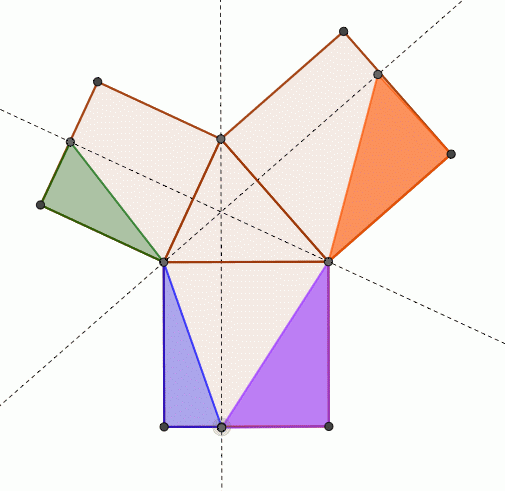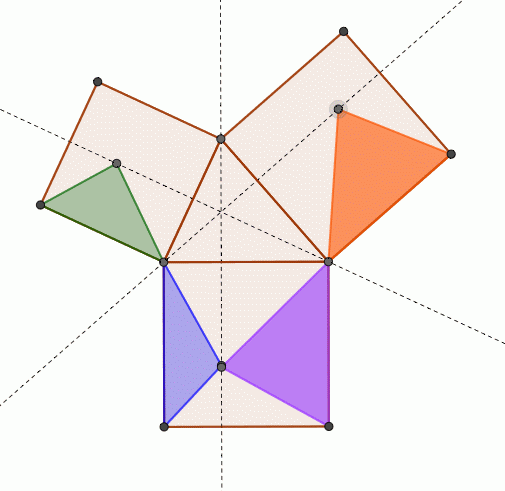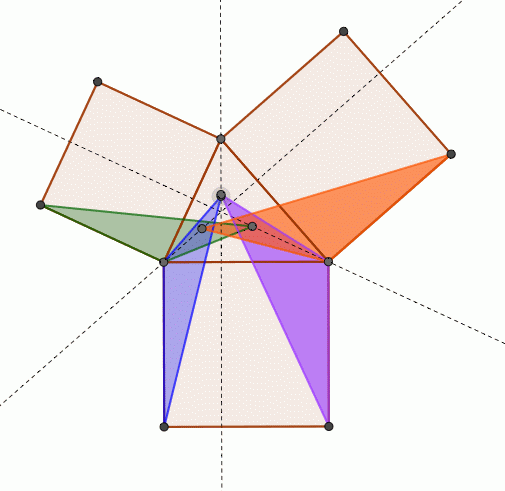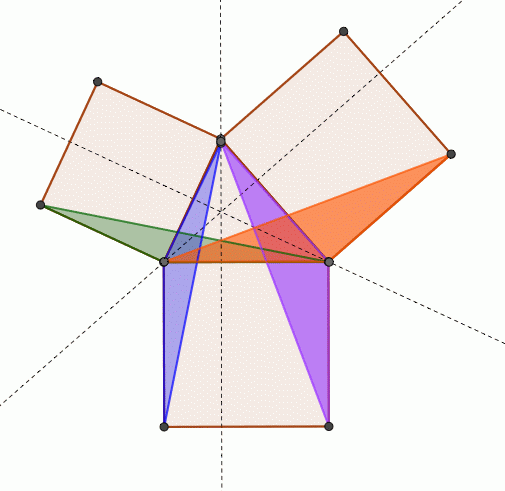
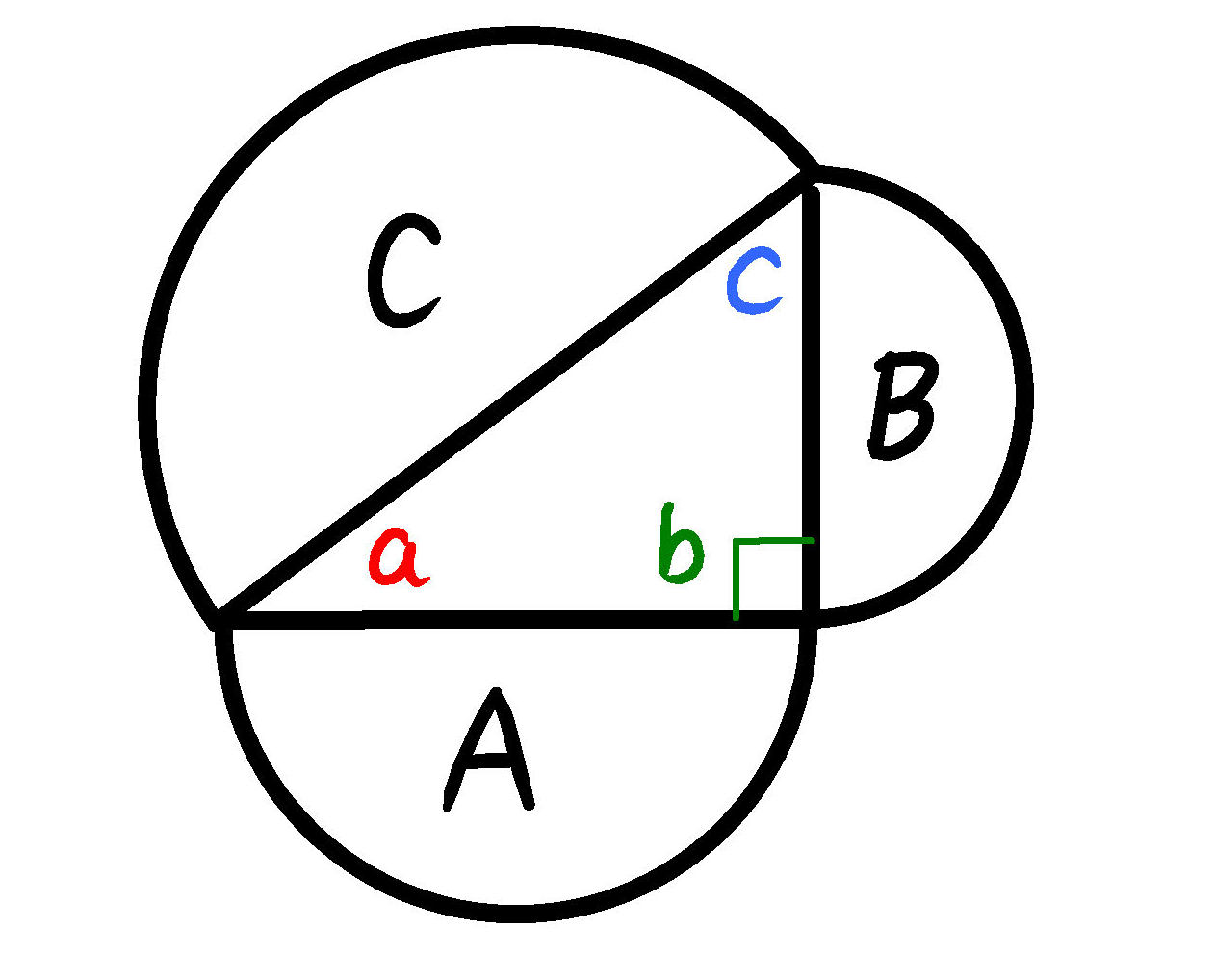
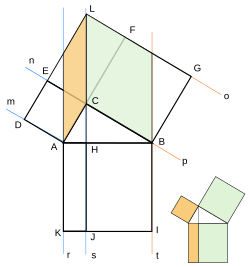
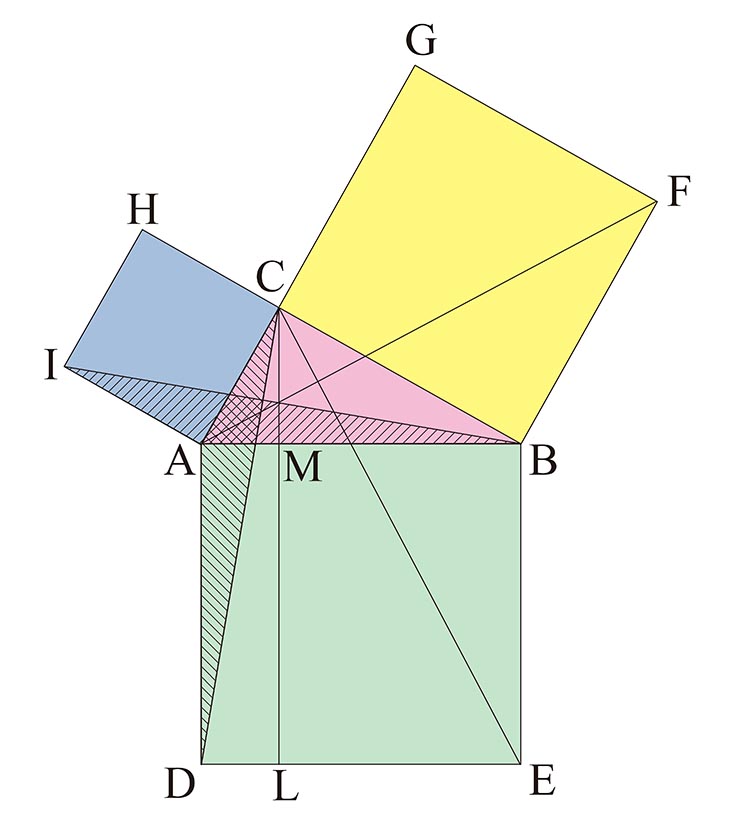
>この定理が何故「ピタゴラスの定理」というのかが分かりません。 N 次元空間 V の中で、 Σn=1~N(,X) と X-Σn=1~N(,X) の組を基底とする 2 次元部分空間を考えてみましょう。 教科書には簡単な証明が載っており、 「f が直交変換ならば、明らか森下四郎『ピタゴラスの定理100の証明法 幾何の散歩道』プレアデス出版、10年8月、改訂版。 isbn 。 森下四郎『ピタゴラスの定理をめぐる2つの謎 三平方の定理の謎』プレアデス出版、10年12月。 isbn 。 関連項目三平方の定理の証明って意外と簡単ですね。 ABCと ACHが相似だから b:AH=c:b 即ち AH=b 2 ABCと CBHも相似だから a:bH=c:a 即ち BH=a 2 だから c=AH+BH=b 2 2 2 +b 2 =c 2 三平方の定理の証明方法は100通り以上あるようです。私自身そんなには知りませんが
ピタゴラスの定理 証明 簡単のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 | ||
 |  |  |
「ピタゴラスの定理 証明 簡単」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
「ピタゴラスの定理 証明 簡単」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「ピタゴラスの定理 証明 簡単」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「ピタゴラスの定理 証明 簡単」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 | ||
「ピタゴラスの定理 証明 簡単」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「ピタゴラスの定理 証明 簡単」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「ピタゴラスの定理 証明 簡単」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「ピタゴラスの定理 証明 簡単」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「ピタゴラスの定理 証明 簡単」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「ピタゴラスの定理 証明 簡単」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「ピタゴラスの定理 証明 簡単」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |
この記事ではこんなことを書いています 数ある数学の公式の中で、面白く、そして美しい公式を紹介します。 面白い数学公式①:オイラー積の公式 オイラー積の公式 \begin{align} \sum_n \frac{1}{n^s} & = \prod_p \frac{1}{1\frac{1}{p^s}} \\ \\ n & = 1, 2, 3, \cdots \\ p & = 2, 3, 5, 7, 11, 13, 17, \cdots \\ s & = \text{\(2\)以上のピタゴラスの定理の証明 簡単にいうと、「2つの量 a と b が共測であるとは、a b が自然数の比 m n で表わせること」となります。定理 B はギリシアの幾何学では、次のように表現されなければなり
Incoming Term: ピタゴラスの定理 証明 簡単,
コメント
コメントを投稿